Let’s start by dissecting the title, since it’s quite a mouthful one! First thing first, I am dealing with a turbulent flow then I am solving a scalar equation and I got to code something, so UDF stuff! It might sound a bit daunting, but it is rather a simple problem, yet the typical written resources are all over the place. I decided to gather bits and pieces from here and there and put everything into a step-by-step and easy-to-follow blog post.
What’s the problem?
I am simulating a turbulent gas-liquid system and the gas bubbles, let’s say they are pure oxygen bubbles, dissolve into the liquid, water for example. To take care of the two phases I can simply use Eulerian-Eulerian framework in Fluent and that’s well documented. So no need to talk about it!
Now I need to do something with the fact that oxygen is diffusing into the water.
A straightforward method is to use the species transport equation
already available in Fluent, and possibly make my life easier. I would just go over
define/models/species to enable it and ask Fluent nicely to solve the
following equation:
In this equation \(Y_i^q\) is the mass fraction of oxygen in phase \(q\) and I have to figure out what to do with the right hand side of the equation. Let’s make it a bit simpler and assume there is no chemical reactions in the system producing oxygen, then the second term with \(R_q^i\) is gone. Also there isn’t any external sources of \(O_2\) and I can cross out \(S_q^i\). The last term on the RHS tells me about the transfer of oxygen at the interface. This can be closed by knowing or calculating the overall mass transfer coefficient, \(k_l\), and the available interfacial area, \(a\), which is another story for itself perhaps for another time. I have left with only the first term on RHS. This represents the diffusion flux of \(O_2\) because of concentration gradient at the interface. Fluent uses Fick’s law to deal with this term and for a turbulent flow the following formulation is applied:
\[\vec{J}_{q}^{i} =-\left(\rho D_{i, lam}+\frac{\mu_{t}}{Sc_{turb}}\right) \nabla Y_{q}^{i}~~~(2)\]This expression accounts for laminar, \(D_{i,lam}\), and turbulent diffusion, \(D_{i,turb}\), coefficients and that is what I am trying to code into Fluent. This is the problem that I am trying to address and I can now go over how to actually solve it.
Do I need to write my own UDF?
Yes! but it’s easy.
Instead of enabling the species equation, I focus on formulating the diffusion of oxygen into the system by solving two User Defined Scalars or in short UDSs. One for the mass fraction of oxygen in the gas bubbles and the second one for the mass fraction of \(O_2\) in liquid phase. The general form of an UDS for a multiphase system reads as below:
\[\frac{\partial}{\partial t}\left(\alpha_{l} \rho_{l} Y_{l}^{O_{2}}\right)+\nabla \cdot\left(\alpha_{l} \rho_{l} U_{l} Y_{l}^{O_{2}}\right)=\nabla \cdot\left(\alpha_{l} \rho_{l} D_{eff}^{O_{2}} \nabla Y_{l}^{O_{2}}\right)+S_{l}^{O_{2}}~~~(3)\]As there is no resistance for the diffusion of oxygen within the bubble, the diffusion term for the mass fraction of oxygen in bubble is neglected. However, for the liquid phase I need to define the diffusion coefficient. Another important point to remember is that the UDS equation in Fluent is always solved for laminar flow and since I am dealing with a turbulent system I should modify the diffusion term in the UDS equation. I decompose the diffusion into the laminar and turbulent components:
\[D_{eff} = D_{lam} + D_{turb}~~~(4)\]The \(D_{lam}\) term is what I read from reference books. For example table 6 on Compilation of Henry’s law constants for water as solvent by Sander defines the value of \(D_{lam}\) according to different measurements. The turbulent diffusion coefficient is formulated based on turbulent Schmidt number, \(Sc_{turb}\):
\[Sc_{turb} = \frac{\mu_t}{\rho D_{turb}}~~~(5)\]Replacing Eq. 5 into Eq. 4, I can re-write the effective diffusion coefficient:
\[D_{eff} = D_{lam} + \frac{\mu_t}{\rho Sc_{turb}}~~~(6)\]This is now pretty clear because as long as I know \(Sc_{turb}\) and \(\mu_t\) then
the effective turbulent diffusion is computed seamlessly. I use Fluent macro
C_MU_T(c,t) to retrieve the value of turbulent viscosity. For the turbulent
Schmidt number, I can use the recommended value for of \(0.7\) for \(k-\varepsilon\)
model or \(1\) for \(RSM\).
There is one last point before coding \(D_{eff}\). Looking at Fluent material properties menu:
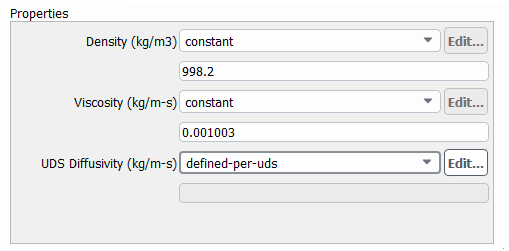
The diffusivity unit is \(kg/m \cdot s\) that tells me Fluent multiply the diffusion coefficient by density. So the final form of the expression for \(D_{eff}\) is:
\[D_{eff} = \rho D_{lam} + \frac{\mu_t}{Sc_{turb}}~~~(7)\]The simplest way to start writing a UDF is to search through the UDF manual and
most probably you find something that is very
similar to what you want. So I also did that and I found DEFINE_DIFFUSIVITY
macro that does exactly what I want. I build up my code based on the example
provided by the manual. The final UDF looks like below and I’ve added extensive
comments to explain what each line is doing.
DEFINE_DIFFUSIVITY(uds_diff_coeff,c,t,i)
{
/* Note: the diffusivity in GUI requires rho*D */
real schmidt, D_turb, D_eff, mu_turb;
/* assign D_eff as laminar diff coeff based on Sander book for O2*/
D_eff = 2.1e-9;
/* Multiply this by the density, C_R(c,t): retrieve density */
D_eff *= C_R(c,t);
/* If turbulence is off, then mu_turb = 0.0, and D_eff = D_lam */
if (rp_turb)
{
/* Turbulent viscosity */
mu_turb = C_MU_T(c,t);
/* Schmidt number */
schmidt = 0.7;
/* Turbulent diffusivity (* rho) based on Sc number for k-e */
D_turb = mu_turb / schmidt;
/* Effective diffusivity (* rho): summation of laminar and turbulent */
D_eff += D_turb;
}
return D_eff;
}
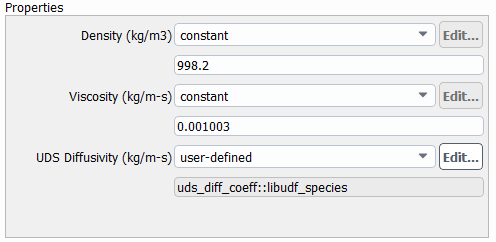
After compiling, the UDF name in this case uds_diff_coeff shows up on the
material properties window where I can hook it up to the calculations.
Remarks or what did I say?
- Species diffusion can be solved using different UDSs in Fluent.
- UDS is solved for laminar flow in Fluent.
- Diffusivity is multiplied by density.
- UDF is required to modify diffusion coefficient.